特征工程之特征选择

​

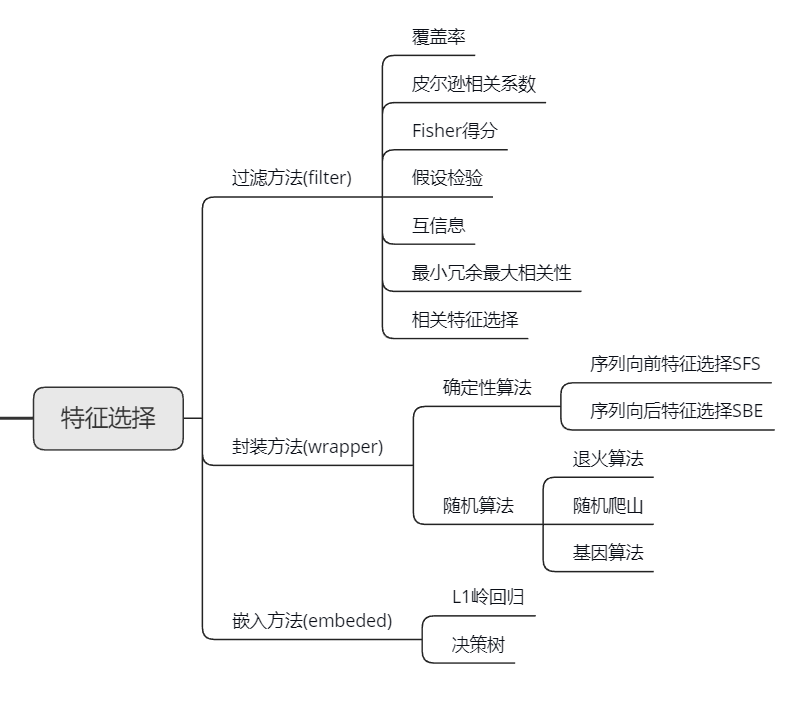
特征选择，即对于生成的特征集合进行筛选，得到一个子集，主要有一下三个目的

• 简化模型，增加可解释性
• 改善性能，并且节省存储空间和计算开销
• 改善通用性，降低过拟合风险。

特征选择主要分为三种方法，过滤方法、封账方法和嵌入方法

过滤方法Filter

过滤方法主要特点：

• 不依赖与机器学习算法
• 一般分为单变量和多变量
• 单变量一般基于特征变量与目标变量之间的相关性或互信息，根据相关性排序，过滤掉最不相关特征
• 多变量有基于相关性和一致性的特征选择

单变量

覆盖率

一般来说，会把缺失率15%-20%左右的特征丢弃掉，不过不是绝对的，也可以通过其他特征的关系或者利用模型预测对缺失值进行补齐。

cols = data.columns.values.tolist()
missing_rate = pd.DataFrame({'column_name':cols})
for c in cols:
    missing_rate.loc[missing_rate['column_name']==c,'missing_rate'] = data[data[c].isna()==True].shape[0]/data.shape[0]

皮尔逊相关系数

皮尔逊相关性系数用于度量两个变量$X$和$Y$的线性相关性，计算公式为

$$\rho_{X,Y}=\frac{cov(X,Y)}{\sigma_X\sigma_Y}$$

样本上的相关性系数为

$$r=\frac{\sum_{i=1}^n(X_i-\bar X_i)(Y_i-\bar Y_i)}{\sqrt{(\sum_{i=1}^n(X_i-\bar X_i)^2)}\sqrt{(\sum_{i=1}^n(Y_i-\bar Y_i)^2)}}$$

在数据标准化（ ）后，Pearson相关性系数、Cosine相似度、欧式距离的平方可认为是等价的。

如何理解皮尔逊相关系数（Pearson Correlation Coefficient）？ - 微调的回答 - 知乎 https://www.zhihu.com/question/19734616/answer/349132554

使用方法

from scipy.stats import pearsonr

r,p = pearsonr(X,Y)

r表示相关性系数

• r>0表示正相关
• r=1表示正线性相关
• r<0表示负相关
• r=0表示非线性相关。
• r=-1表示负线性相关

p-value越低表示越低，可靠性越高。https://www.cnblogs.com/lijingblog/p/11043513.html

Fisher得分

在分类问题中，对于好的特征，在同一类别中取值比较相似，在不同类别中取值差异较大。因此特征i的重要性可以用Fisher得分$S_i$表示：

$$S_i=\frac{\sum_{j=1}^Kn_j(u_{ij}-u_i)^2}{\sum_{j=1}^Kn_j\rho^2_{ij}}$$

$u_{ij}$和$\rho_{ij}$分别表示特征$i$在类别$j$中的中的均值和方差，$n_j$表示类别$j$的样本数，Fisher特征越高，特征在不同类别的差异性越大，在同一类别的差异性越小。

卡方检验

目的：检验特征变量和目的变量之间的相关性

公式为：

$$\chi^2=\sum_{i=1}^r\sum_{j=1}^c\frac{(O_{i,j}-E_{i,j})^2}{E_{i,j}^2}$$

其中$O_{i,j}$表示观测值，$E_{i,j}$表示期望值，$i$表示类别$i$，$j$表示对应的目标变量$j$。如何假设正确，$\chi$越小，相关性越小。

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from sklearn.datasets import load_iris

iris = load_iris()
model1 = SelectKBest(chi2, k=2)#选择k个最佳特征
model1.fit_transform(iris.data, iris.target)

互信息

用于度量两个变量之间的相关性，互信息越大，表示两个变量的相关性越高，互信息为0，表示两个变量相互独立。

互信息计算公式：

$$I(X,Y)=\sum_{x\in X}\sum_{y\in Y}p(x,y)log\frac{p(x,y)}{p(x)p(y)}$$

其中$X、Y$的联合分布为$p(x,y)$，边缘分布为$p(x),p(y)$。

from sklearn import metrics as mr
mr.mutual_info_score(Y,X)

多变量

最小冗余最大相关性mRmR

相关特征选择(CFS)

相关特征选择(Correlation Feature Selection，CFS)基于以下假设来评估集合的重要性：好的特征集合包含于目标变量非常相关的特征，但这些特征彼此不想关。

公式如下：

$$CFS=\max_{S_k}[\frac{r_{cf_1}+r_{cf_2}+...+r_{cf_k}}{\sqrt{k+2(r_{f_1f_2}+r_{f_if_j}+...+r_{f_kf_1})}}$$

其中$r_{cf_i}$和$r_{f_if_j}$分别表示特征变量和目标变量之间的相关性以及特征变量与特征变量之间的相关性。

这部分代码暂时没有搞懂，后续在研究。

import numpy as np
from skfeature.function.statistical_based import CFS
from sklearn.datasets import load_iris  # 利用iris数据作为演示数据集

# 载入数据集
iris = load_iris()
X, y = iris.data, iris.target
train_set = X[0:100,:]
test_set = X[100:,]
train_y = y[0:100]

num_feature = 2 # 从原数据集中选择两个变量

feature_index = CFS.cfs(train_set, train_y)

FCBF

FCBF算法： 全称 Fast Correlation-Basd Filter Solution, 是一种快速过滤的特征选择算法，一种基于symmetrical uncertainty（SU）的方法。其计算步骤如下：

1、计算每个特征与目标C之间的相关性$SU_{F_i,c}$

$$SU(X,Y)=2\frac{IG(X,Y)}{E(X)+E(Y)} \\E(x)=-\sum_{i=1}^cPx_i()*\log_2(P_{X_i}) \\E(X|Y)=-\sum_{i=1}^{C_Y}P(y_i)\sum_{j=1}^cP(x_j|y_i)\log_2(P(x_j|y_i))$$

其中$IG(X,Y)$代表信息增益，$E(X)$代表信息熵，$P(X_i)$表示$X$取到$i$的概率，$c$为类别数目

2、将最大相关性的特征预先使用$\delta$选择出来

3、将$SU_{F_i,c}$按照大小排序，并且计算每个特征$F_i$与排序中SU小于$SU_{}$的特征$F_j$之间的相关性$SU_{F_i,F_j}$，如果$SU_{F_i,c}>SU_{F_j,c}$,计算$SU_{F_i,F_j}$

4、如果$SU_{F_i,F_j}>SU_{F_j,c}$，删除特征$F_j$

封装方法Wrapper

封装方法直接利用机器学习算法评价特征子集的效果，它可以检测两个或者多个特征之间的相互关系，而且选择的特征子集让模型效果运行达到最优

确定性算法

序列前向特征选择(SFS)和序列后向特征选择(SBE)

序列向前算法，特征子集从空集开始，每次只加入一个特征，

随机算法

退火算法

遗传算法

遗传算法步骤：

1、初始化种群

一个种群有好几条染色体，假设有m个初始特征，那么染色体为一个m*1的一维向量[0,1,0,1,….1]，全部由0或者1组成，初始化时，0和1随机选择。

2、评估种群中个体适合度

用交叉检验cross_val_score(个体，y)的结果作为适应度。适应度计算类似LDA

3、选择

每条染色体的适应度不同，被选择的概率也不同，用轮盘赌选择，先生成与染色体个数相同的随机数个数，先生成与染色体个数（种群大小）相同的随机数然后再一个个看这些随机数落在哪个染色体的范围内
例：
染色体的选择概率：①[0,0.3), ②[0.3,0.6), ③[0.6,0.7), ④[0.7,0.9), ⑤[0.9,1]
生成的随机数：0.2, 0.4, 0.5, 0.78, 0.8
被选中的染色体：①, ②, ②, ④, ④

5、交叉

若第i条与第i+1条染色体发生交叉，随机选择交叉点，然后交叉。

例如

父染色体

a:[0,1,0,0,1]

b:[1,0,1,1,1]

交叉之后的染色体为[0,1,0,1,1]

6、变异

染色体的某个点取反。目的是防止局部最优

蚁群算法

蚁群算法的基本思想：

1、蚂蚁在路径上释放信息素。

2、碰到还没走过的路口，就随机挑选一条路走。同时，释放与路径长度有关的信息素。

3、信息素浓度与路径长度成反比。后来的蚂蚁再次碰到该路口时，就选择信息素浓度较高路径。

4、最优路径上的信息素浓度越来越大。

5、最终蚁群找到最优寻食路径。

嵌入方法Embedded

嵌入方法将特征选择嵌入到模型的构建过程当中，具有封装方法与机器学习方法相结合的有点，而且具有过滤方法计算效率高的有点，避免了前面两种方法的不足。

LASSO方法

及线性回归+L1范数，具体原理就不细讲了。

from sklearn.linear_model import Lasso
from sklearn.preprocessing import StandardScaler
from sklearn.datasets import load_boston

boston = load_boston()
scaler = StandardScaler()
X = scaler.fit_transform(boston["data"])
Y = boston["target"]
names = boston["feature_names"]

lasso = Lasso(alpha=.3)
lasso.fit(X, Y)

基于树模型的特征选择

树模型本身可以进行特征选择，配合sklearn中的SelectFromModel可以进行特征选择。

1、结合SelectFromModel

SelectFromModel的作用是训练基础模型，得到系数较高的特征

from sklearn.feature_selection import SelectFromModel
from sklearn.ensemble import GradientBoostingClassifier
from sklearn.datasets import load_iris 

iris = load_iris()
gbdt = GradientBoostingClassifier()
SelectFromModel(gbdt).fit_transform(iris.data,iris.target)

2、结合相关系数

主要分为一下几步：

• 第一次训练lightGBM，得到特征重要性
• 挑选重要性比较高的特征，计算特征相似度，热力图也行
• 筛选掉相似度过高的特征
• 将筛选之后的特征送入lightGBM重新训练

参考资料

1、https://www.cnblogs.com/hhh5460/p/5186226.html

2、https://www.kaggle.com/juliaflower/feature-selection-lgbm-with-python/comments

3、美团机器学习实践

4、https://blog.csdn.net/u012017783/article/details/71872950

5、https://www.cnblogs.com/holaworld/p/12631851.html

6、https://zhuanlan.zhihu.com/p/33042667

7、https://www.cnblogs.com/heaad/archive/2010/12/20/1911614.html

8、https://www.cnblogs.com/holaworld/p/12631933.html